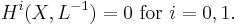Mumford vanishing theorem

In algebraic geometry, the Mumford vanishing theorem Mumford (1967) states that if L is a semi-ample invertible sheaf with Iitaka dimension at least 2 on a complex projective manifold, then

$H^i(X,L^{-1})=0\text{ for }i = 0,1.\$

The Mumford vanishing theorem is related to the Ramanujam vanishing theorem, and is generalized by the Kawamata–Viehweg vanishing theorem.

References

Kawamata, Yujiro (1982), "A generalization of Kodaira-Ramanujam's vanishing theorem", Mathematische Annalen 261 (1): 43–46, doi:10.1007/BF01456407, ISSN 0025-5831, MR 675204, http://dx.doi.org/10.1007/BF01456407
Mumford, David (1967), "Pathologies. III", American Journal of Mathematics (The Johns Hopkins University Press) 89 (1): 94–104, doi:10.2307/2373099, ISSN 0002-9327, JSTOR 2373099, MR 0217091